Mathematical Notation for Recommender Systems
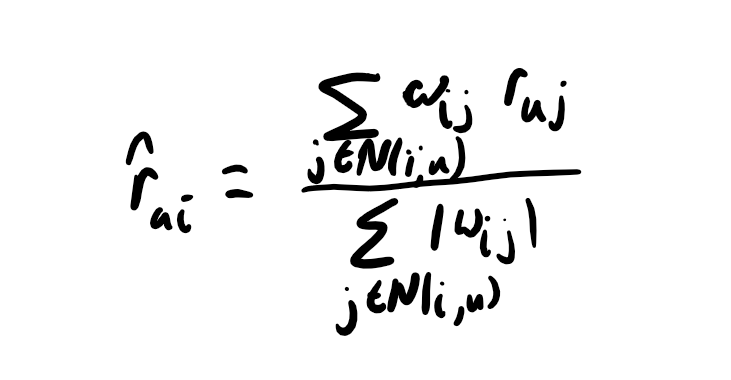
Over the years of teaching and research, I have gradually standardized the notation that I use for describing the math of recommender systems. This is the notation that I use in my classes, Joe Konstan and I have adopted for our MOOC, and that I use in most of my research papers. (And thanks to Joe for helping revise it to its current form.)
If you haven’t already settled on a notation, perhaps you would consider adopting this one. I also welcome feedback on improving it.
I have tried to strike a balance between clarity and clutter. I slightly overload the meaning of some symbols; in particular, I am loose with distinctions between sets and matrices, because it is generally clear from context which is being invoked; I do not overload external referents, however. I also have tried to keep this notation so that it can be hand-written, making it more useful in teaching but meaning that I cannot rely as much on typography to distinguish different objects (e.g. separating \(U\) and \(\mathcal{U}\) would be questionable).
Input Data
Our input data, for collaborative filtering, consists of:
- \(U\)
- The set of users in the system or data set.
- \(I\)
- The set of items in the system or data set.
- \(R\)
- The set of ratings in the data set. \(R\) can be used as either a set of rating observations or as a (partially observed) \(|U| \times |I|\) matrix; context makes it clear which meaning is intended.
Within each of these sets, we can refer to individual entries:
- \(u, v \in U\)
- I use \(u\) and \(v\) as variables referencing individual users. If I need more than two, then I use numeric subscripts \(u_1\), \(u_2\), etc.
- \(i, j \in I\)
- I use \(i\) and \(j\) as variables referencing individual items. Again, for more than two, I use numeric subscripts. This does mean that \(i\) is not available as a counter variable, but I do not find that to be too much of a difficulty in practice.
- \(r_{ui} \in R\)
- An individual rating value, the rating user \(u\) gave for item \(i\). In an implicit feedback setting, this takes on whatever value you are using as the ‘rating’: 1/0, a play count, etc.
One advantage of always using \(u,v\) for users and \(i,j\) for items is that meaning is clear from looking at a variable or subscripted variable. It also allows the following subset notations:
- \(I_u \subset I\)
- The set of items rated by user \(u\).
- \(U_i \subset U\)
- The set of users who have rated or purchased item \(i\).
- \(R_u \subset R\)
- The set of ratings given by user \(u\)
- \(R_i \subset R\)
- The set of items for item \(i\)
- \(\vec{r}_u\)
- User \(u\)’s rating vector, an \(|I|\)-dimensional vector with missing values for unrated items.
- \(\vec{r}_i\)
- Item \(i\)’s rating vector, a \(|U|\)-dimensional vector with missing values for users who have not rated the item.
Scores and Similarities
With this notation, we can write things like the user-user rating prediction formula:
\[\hat r_{ui} = s(i;u) = \frac{\sum_{v \in N(u,i)} w(u,v)(r_{vi}-\bar r_v)}{\sum_{v \in N(u,i)} |w(u,v)|} + \bar r_u\]
\(N(u;i)\) is the neighborhood for user \(u\) for the purpose of scoring item \(i\), and \(\bar r_u\) is user \(u\)’s average rating. I explicitly state the ranges of my summations for two reasons, even if they are implicitly clear for experienced recsys researchers: it is a common tripping point for students, and it is a place where subtle implementation differences get buried. I find that it is not overly cumbersome with this notation.
Matrix Factorization
For basic decomposition of the ratings matrix, I usually use \(P\) and \(Q\) these days:
\[R \approx PQ^{\mathrm{T}}\]
We then have user vectors \(\vec p_u\) and item vectors \(\vec q_i\). I like using the transpose notation for the factorization, so that latent features are on the columns of both \(P\) and \(Q\).
Advanced decompositions that involve more than two matrices will need to find additional matrices; one unfortunate tradeoff of using \(U\) for the set of users is that it is no longer available for a matrix.